FHQ-Treap

Treap

Treap 是一种平衡树。每个点除了维护这个点的权值（$val$）以外，还维护一个随机的优先级（$priority$）。其中权值满足二叉搜索树的性质，优先级满足堆的性质，即：

• 左子树权值 $\le$ 父节点权值 $\le$ 右子树权值（二叉搜索树性质）；
• 父节点优先级 $\le$ 子节点优先级（堆性质，如果使用小根堆）。

若每个节点的优先级都随机生成，则树的形态也是随机的。一棵随机树的期望高度是 $O(\log n)$ 的，因此 Treap 的期望高度是 $O(\log n)$。

FHQ-Treap

FHQ-Treap（无旋式 Treap），通过开裂和合并，完成平衡树的操作，并保持树满足堆的性质。

接下来以 洛谷 P3369 普通平衡树 为例，讲解 FHQ-Treap 的基本操作。

定义节点

int root, tot; // 根节点编号、节点数量
struct tree
{
    int val, pri; // 权值、优先级
    int ls, rs; // 左子树、右子树
    int siz; // 子树大小
} t[N];
void push_up(int o)
{
    t[o].siz = t[t[o].ls].siz + t[t[o].rs].siz + 1;
}

分裂

将一棵 Treap 分裂成两棵树，第一棵树中的权值都 $\le k$，第二棵树中的权值都 $>k$。

递归到节点 $x$ 时：

• 若 $x$ 的权值 $\le k$，则 $x$ 和左子树都会被划分到第一棵树中，右子树的一部分被划分到第一棵树中，另一部分被划分到第二棵树中。
• 若 $x$ 的权值 $> k$，则 $x$ 和右子树都会被划分到第二棵树中，左子树的一部分被划分到第一棵树中，另一部分被划分到第二棵树中。

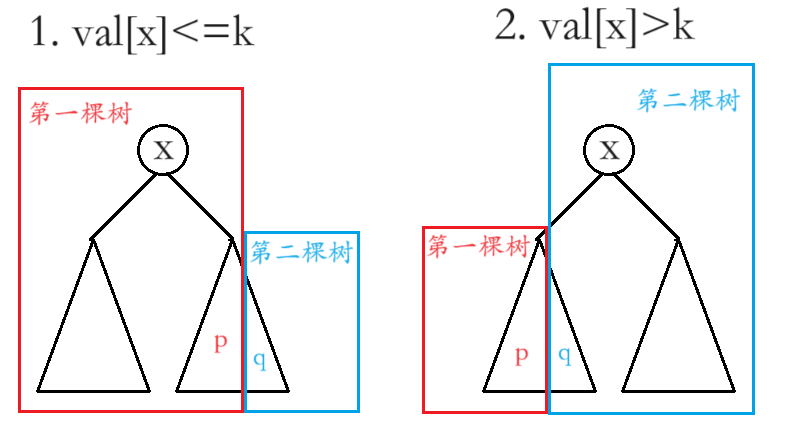
第一种情况：继续分裂 $x$ 的右子树，设分裂成 $p$ 和 $q$。将 $x$ 设为第一棵树的根，它的左子树不变，右子树设为 $p$。将 $q$ 设为第二棵树。

第二种情况：继续分裂 $x$ 的左子树，设分裂成 $p$ 和 $q$。将 $x$ 设为第二棵树的根，它的右子树不变，左子树设为 $q$。将 $p$ 设为第一棵树。

void split(int o,int x,int &l,int &r)
{
    if(!o)
    {
        l = r = 0;
        return;
    }
    // 如果有标记，在这里push_down(o)
    if(t[o].val<=x) 
    {
        l = o;
        split(t[o].rs, x, t[o].rs, r);
    }
    else
    {
        r = o;
        split(t[o].ls, x, l, t[o].ls);
    }
    push_up(o);
}

合并

假设现在有两棵 Treap $p,q$，且满足 $p$ 中所有节点的权值都小于等于 $q$ 中所有节点的权值，那么我们可以将这两棵树合并成一棵树。

合并的过程中要保持树满足堆的性质。所以我们要比较 $p$ 和 $q$ 的优先级大小。

• 若 $p$ 优先级小，则 $p$ 作为新树的根，把 $p$ 的右子树和 $q$ 合并起来。
• 若 $q$ 优先级小，则 $q$ 作为新树的根，把 $q$ 的左子树和 $p$ 合并起来。

int merge(int x,int y)
{
    if(!x || !y)
        return x + y;
    if(t[x].pri<=t[y].pri)
    {
        // 如果有标记，在这里push_down(x)
        t[x].rs = merge(t[x].rs, y);
        push_up(x);
        return x;
    }
    else
    {
        // 如果有标记，在这里push_down(y)
        t[y].ls = merge(x, t[y].ls);
        push_up(y);
        return y;
    }
}

插入

假设我们要将 $x$ 插入到平衡树中。

我们可以先将平衡树分裂成 $l,r$，其中 $l$ 中所有节点权值都 $\le x$，$r$ 中所有节点权值都 $> x$。

然后新建一个独立的节点，权值为 $x$。然后我们将 $l$、新建的节点、$r$ 合并起来，就做完了。

int new_node(int x)
{
    tot++;
    t[tot].val = x;
    t[tot].pri = rnd(); // 优先级取随机数
    t[tot].siz = 1;
    return tot;
}
void add(int x)
{
    int l, r;
    split(root, x, l, r);
    int p = new_node(x);
    root = merge(merge(l, p), r);
}

删除

假设我们要删除 $x$ 这个数字。

我们通过两次分裂操作，将平衡树分裂成三部分：$<x$、$=x$ 和 $>x$ 的部分。

我们可以删除 $=x$ 部分的任意一个节点。最方便的是删除这部分的根节点，将根节点的左右子树合并起来即可。

最后不要忘记将这三部分合并起来。

void del(int x)
{
    int l, p, r; // 分别表示 <x、=x、>x 的部分
    split(root, x, l, r);
    split(l, x - 1, l, p);
    p = merge(t[p].ls, t[p].rs);
    root = merge(merge(l, p), r);
}

根据值查询排名

操作等价于：给定 $x$，求比 $x$ 小的数字个数 $+1$。

那么我们可以将 $<x$ 的部分分裂出来，然后查询这部分的大小即可。

int rank(int x)
{
    int l, r;
    split(root, x - 1, l, r);
    int ans = t[l].siz;
    root = merge(l, r);
    return ans + 1;
}

根据排名查询值

和二叉搜索树求第 $k$ 小值的方法差不多。将左子树的大小与 $k$ 比较，判断第 $k$ 小的节点在左子树中、在右子树中、还是在根节点上即可。

int kth(int o,int k)
{
    if(t[t[o].ls].siz > k - 1) return kth(t[o].ls, k); // 第 k 小值在左子树中
    else if(t[t[o].ls].siz == k - 1) return t[o].val;  // 第 k 小值为根节点
    else return kth(t[o].rs, k - t[t[o].ls].siz - 1);  // 第 k 小值在右子树中
}

查询前驱

即查询比 $<x$ 的数字的最大值。

我们将 $<x$ 的部分分裂出来，不停向右子树走就可以走到这部分的最大值。

int pre(int x)
{
    int l, r;
    split(root, x - 1, l, r);
    int pos = l;
    while(t[pos].rs) pos = t[pos].rs; //只要这个节点有右子树，就向右子树跳
    int ans = t[pos].val;
    root = merge(l, r);
    return ans;
}

查询后继

与前期类似，我们查询的是 $>x$ 的数字的最小值。

我们将 $>x$ 的部分分裂出来，不停向左子树走就可以走到这部分的最小值。

int nxt(int x)
{
    int l, r;
    split(root, x, l, r);
    int pos = r;
    while(t[pos].ls) pos = t[pos].ls; //只要这个节点有左子树，就向左子树跳
    int ans = t[pos].val;
    root = merge(l, r);
    return ans;
}

科技：合并两棵没有大小关系的树

时间复杂度两个 $\log$，但是我不会证明。

int Merge(int x,int y)
{
    if(!x || !y) return x + y;
    if(t[x].pri > t[y].pri) swap(x, y);
    // 此时 t[x].pri <= t[y].pri，我们考虑将 y 合并到 x 上
    // push_down(x);
    int l, r;
    split(y, t[x].val, l, r); // 将 y 分裂成两棵树
    t[x].ls = Merge(t[x].ls, l); // 将 y 中 <=t[x].val 的部分合并到 x 的左子树
    t[x].rs = Merge(t[x].rs, r); // 将 y 中 >t[x].val 的部分合并到 x 的右子树
    push_up(x);
    return x;
}

----------待更新----------