二分图匹配，霍尔定理

霍尔定理

霍尔定理给出了，二分图左侧的点能全部匹配上的充要条件：

记

• 二分图左侧的点集为 $L$，右侧的点集为 $R$。
• 点集 $S$ 为 $L$ 的一个子集。
• $N(S)$ 表示与 $S$ 中的点有连边的点的集合。显然 $N(S)$ 为 $R$ 的子集。

则二分图左侧的点能全部匹配上的充要条件是：

• 对于任意 $S$，有 $|N(S)|\ge|S|$。

证明

还不会（

【Luogu P3488】LYZ-Ice Skates

题目链接

将每一个人与他能穿上的鞋子连一条边，要求的就是：是否所有人都能匹配上。

显然可以使用霍尔定理。如果存在一个 $S$，使得 $|N(S)|<|S|$，那么就不合法。否则合法。

我们考虑计算：是否存在 $S$，使得 $|S|-|N(S)| > 0$。

首先，如果 $S$ 中的两个尺码差距 $\le d$，那么可以将它们中间的尺码全选上。此时 $|S|$ 不变，$|N(S)|$ 变小，所以 $|S|-|N(S)|$ 一定不会变小。如下图：

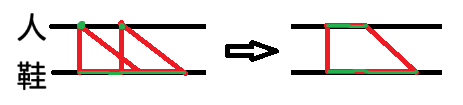
这样操作后，选取的结果一定构成一些没有交点的梯形。要判断总的 $|S|-|N(S)|$ 是否为正，我们判断是否有其中一个梯形的 $|S|-|N(S)|$ 为正即可。

设尺码为 $i$ 的人数为 $a_i$，则尺码区间为 $[l,r]$ 的梯形的 $|S|-|N(S)|$ 即为：

$$\left(\sum_{i=l}^r a_i-k\right)-d\cdot k$$

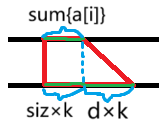
我们发现，只需要对 $a_i-k$ 维护最大子段和即可。